Pesquisa Binária
Podemos definir o problema da pesquisa binária como a seguir:
-
Descrição da entrada: Uma sequência ordenada $S$ de $n$ números e um elemento $e$ que desejamos encontrar.
-
Descrição da tarefa: Determinar se o elemento $e$ está na sequência $S$.
-
Descrição da saída: Se o elemento estiver na sequência, retorne o índice em que o elemento $e$ aparece em $S$. Caso contrário, retorne o valor $-1$.
Anteriormente, vimos como percorrer um vetor linearmente, ou seja, posição por posição, procurando por um elemento. Essa estratégia funciona bem para vetores pequenos, mas ela é impraticável para vetores grandes. Usar essa estratégia para pesquisar em um vetor com muitos elementos seria o equivalente de procurar pelo número do telefone de alguém percorrendo página por página de uma lista telefônica. Com a pesquisa binária, o tempo de se pesquisar por um elemento em um vetor ordenado (como uma lista telefônica, por exemplo) é drasticamente reduzido. Vejamos como esse tipo de pesquisa funciona.
Considerando ainda o exemplo da lista telefônica, suponha que você deseja encontrar o número do telefone do Paulo. Você abre a lista telefônica mais ou menos na metade e percebe que a página é referente à letra "m". Com essa informação simples, você consegue descartar cerca de metade das páginas da lista telefônica (aquelas que estão antes da página que você abriu). A pesquisa binária utiliza essa ideia de eliminar metades do arranjo a cada passo do algoritmo.
A pesquisa binária (ou busca binária) funciona assim. Começamos com um palpite de onde o elemento procurado pode estar. Nosso palpite é sempre escolher o elemento do meio do arranjo. Se esse palpite estiver certo, a pesquisa termina, pois encontramos o elemento procurado. Se o palpite estiver errado, podemos restringir nosso próximo palpite a uma parte específica do arranjo, dado que ele está ordenado. O raciocínio pode trás disso é que se o elemento procurado for maior que o elemento do meio do arranjo, sabemos que o elemento procurado só pode estar na segunda metade do arranjo. Caso contrário, o elemento procurado só pode estar na primeira metade do arranjo. Esta explicação pode parecer um pouco abstrata, mas ela ficará mais clara com um exemplo.
Suponha que desejemos procurar pelo elemento $83$ em um arranjo com os seguintes elementos: $[1, 3, 45, 59, 60, 83, 90]$. Para simplificar as coisas, dado que não sabemos onde o elemento pode estar, nosso palpite é que ele estará no meio do arranjo (59, no nosso caso). Nosso palpite está errado, mas ainda assim obtemos uma informação importante: como sabemos que o arranjo está ordenado e que o elemento procurado é maior do que o elemento que está no meio do arranjo, o elemento procurado tem que estar na segunda metade do arranjo, ou seja, entre o sub-arranjo $[60, 83, 90]$. A seguir, fazemos um novo palpite de onde o elemento pode estar. Como fizemos anteriormente, nosso palpite é que o elemento procurado está no meio da parte do vetor que estamos considerando (segunda metade do vetor). Dessa vez, nosso palpite está certo: o elemento 83 está no meio da segunda metade do vetor. A figura abaixo ilustra os passos realizados na busca pelo elemento desejado.

No exemplo acima, fomos capazes de encontrar o elemento desejado com apenas duas comparações. Se tivéssemos usado pesquisa linear, teriam sido necessárias cinco comparações para encontrar o elemento desejado. Na prática, usando pesquisa binária em um arranjo ordenado de tamanho $n$, precisamos de no máximo $O(\log n)$ comparações para dizer se um elemento está presente. No exemplo anterior, o número de comparações feitas pela pesquisa binária e pela pesquisa linear parece não ser muito diferente. Mas essa diferença começa a ficar evidente quando consideramos arranjos de tamanhos maiores. A tabela abaixo mostra, para um arranjo de tamanho $n$, o número de comparações feitas pela pesquisa linear e pela pesquisa binária.
| $n$ | Pesquisa Linear | Pesquisa Binária |
|---|---|---|
1024 |
1024 |
10 |
4096 |
4096 |
12 |
16384 |
16384 |
14 |
65536 |
65536 |
16 |
262144 |
262144 |
18 |
Os gráficos a seguir mostram o crescimento da função de complexidade da pesquisa linear ($O(n)$) e da pesquisa binária ($O(\log n)$) à medida em que aumentamos o valor de $n$. Perceba a diferença nos valores do eixo y, que mostram o número de comparações feitas pelo algoritmo para um dado valor de entrada (eixo x), no pior caso.
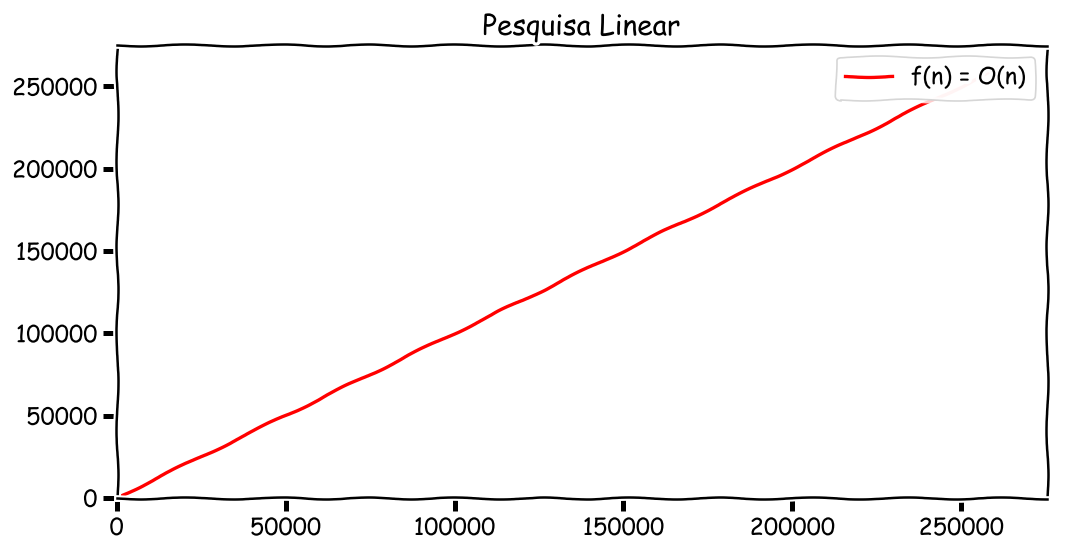
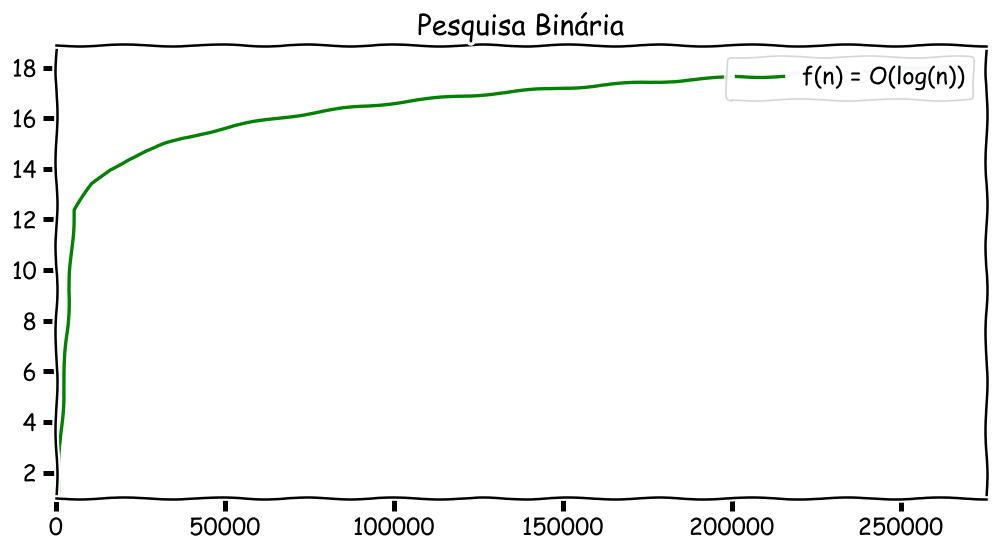
A pesquisa binária apresenta complexidade assintótica inferior à pesquisa linear, permitindo-nos pesquisar por elementos com complexidade logarítmica no tamanho do arranjo, desde que ele esteja ordenado.
A pesquisa binária também é útil em outros cenários. Por exemplo, suponha que nos seja fornecido um arranjo que contém somente os valores $0$ e $1$ e todos os $0$s vêm antes dos $1$s. Se desejarmos saber a posição em que o primeiro $1$ ocorre, podemos usar pesquisa binária. O raciocínio é o mesmo e o algoritmo é bem parecido, exceto por algumas modificações menores. Outros tipos de cenários em que a pesquisa binária pode ser usada serão mostrados nos exercícios.
Agora que já discutimos um pouco da teoria envolvendo pesquisa binária, podemos partir para os detalhes de como implementar o algoritmo.
Primeiro, vamos implementar uma versão recursiva do algoritmo de pesquisa binária. Assim como fizemos nos capítulos anteriores, precisamos determinar:
-
a entrada do algoritmo;
-
a saída do algoritmo;
-
o que faremos caso recebamos como entrada uma lista vazia;
-
e o que faremos caso a lista de entrada não esteja vazia.
A entrada do algoritmo será um arranjo (lista) de números inteiros, o número que desejamos saber se está na lista e os limites do arranjo que analisaremos—chamaremos esses limites de esquerda e direita. Por que esses limites são importantes? Lembre-se que no nosso exemplo acima, a cada etapa do algoritmo eliminamos uma metade do arranjo e analisamos somente a outra metade. Esses limites nos permitem manter um registro de qual parte do arranjo estamos analisando a cada momento.
A saída do algoritmo será o índice do arranjo em que o elemento procurado está, ou o valor -1, caso o elemento não esteja presente no arranjo.
Se nosso algoritmo receber como entrada um arranjo vazio, podemos simplesmente retornar o valor -1.
Se o arranjo de entrada não estiver vazio, vamos implementar a mesma ideia do exemplo acima: precisamos fazer um palpite de onde o elemento desejado está, e caso o elemento não esteja nesta posição, atualizamos os limites esquerdo e direito do arranjo e continuamos nossa busca. Dada esta descrição, veja se você consegue entender a implementação abaixo.
def pesquisa_binaria_recursiva(A, esquerda, direita, item):
"""Implementa pesquisa binária recursivamente."""
# 1. Caso base: o elemento não está presente. (1)
if direita < esquerda:
return -1
meio = (esquerda + direita) // 2
# 2. Nosso palpite estava certo: o elemento está no meio do arranjo. (2)
if A[meio] == item:
return meio
# 3. O palpite estava errado: atualizamos os limites e continuamos a busca. (3)
elif A[meio] > item:
return pesquisa_binaria_recursiva(A, esquerda, meio - 1, item)
else: # A[meio] < item
return pesquisa_binaria_recursiva(A, meio + 1, direita, item)
A = [0, 10, 20, 30, 40, 50, 60, 70]
print("Pesquisa com sucesso:", pesquisa_binaria_recursiva(A, 0, len(A) - 1, 20))
print("Pesquisa com sucesso:", pesquisa_binaria_recursiva(A, 0, len(A) - 1, 0))
print("Pesquisa com sucesso:", pesquisa_binaria_recursiva(A, 0, len(A) - 1, 70))
print("Pesquisa com sucesso:", pesquisa_binaria_recursiva(A, 0, len(A) - 1, 100))Pesquisa com sucesso: 2 Pesquisa com sucesso: 0 Pesquisa com sucesso: 7 Pesquisa com falha: -1
Analisemos a implementação acima para tentarmos entender o que está acontecendo. O algoritmo de pesquisa binária é muito importante, então compensa analisarmos sua implementação em mais detalhes. Perceba que inserimos comentários numerados no código para que possamos nos referir a eles agora em nossa análise da implementação. Vejamos:
| 1 | Caso base: O primeiro comentário no código se refere ao caso base do algoritmo. Se você ainda não sabe o que é isso, leia este artigo. No caso base, verificamos se o elemento procurado não está na lista. Isso ocorrerá quando realizarmos a busca em todas as possíveis posições do arranjo em que o elemento poderia estar e não o encontrarmos. Quando isso acontecer, os limites esquerdo e direito se cruzarão. A verificação no caso base simplesmente checa isso e retorna o valor -1 se os limites tiverem se cruzado. |
| 2 | Palpite: No algoritmo de pesquisa binária, precisamos fazer um palpite de onde acreditamos que o elemento procurado possa estar. Um bom palpite é supormos que o elemento está no meio do arranjo. Com isso, eliminamos metade do arranjo a cada passo da nossa busca. |
| 3 | Elemento procurado não é o elemento no meio do arranjo: Se o elemento não está no meio do arranjo, temos duas opções: ou ele é menor do que o elemento que está no meio, ou ele é maior. Caso ele seja menor do que o elemento que está no meio do arranjo, podemos restringir nossa busca ao intervalo $[0, meio - 1]$. Caso o ele seja maior do que o elemento que está no meio do arranjo, podemos restringir nossa busca ao intervalo $[meio + 1, n]$. Note que isso só é possível porque sabemos que o arranjo está ordenado. |
Uma vez que entendemos como funciona o algoritmo de pesquisa binária, podemos nos fazer outra pergunta: é possível melhorá-lo ainda mais? Embora não seja possível reduzirmos a complexidade assintótica do algoritmo, podemos tentar melhorá-lo de alguma outra forma. Uma possível melhoria é implementarmos uma versão iterativa do algoritmo. Em geral, uma função recursiva consome mais memória que a versão iterativa dessa função, mas há situações em que o uso da recursividade é vantajoso.
Vejamos o código da pesquisa binária iterativa e depois façamos uma análise das diferenças dele para a versão recursiva.
def pesquisa_binaria(A, item):
"""Implementa pesquisa binária iterativamente."""
esquerda, direita = 0, len(A) - 1
while esquerda <= direita:
meio = (esquerda + direita) // 2
if A[meio] == item:
return meio
elif A[meio] > item:
direita = meio - 1
else: # A[meio] < item
esquerda = meio + 1
return -1
A = [0, 10, 20, 30, 40, 50, 60, 70]
print("Pesquisa com sucesso:", pesquisa_binaria(A, 20))
print("Pesquisa com sucesso:", pesquisa_binaria(A, 0))
print("Pesquisa com sucesso:", pesquisa_binaria(A, 70))
print("Pesquisa com sucesso:", pesquisa_binaria(A, 100))Pesquisa com sucesso: 2 Pesquisa com sucesso: 0 Pesquisa com sucesso: 7 Pesquisa com falha: -1
Analisemos a implementação acima para tentarmos entender as diferenças em relação à versão recursiva:
-
Verificação dos extremos do arranjo: assim como na versão recursiva, fazemos uma verificação para saber se os limites esquerdo e direito se cruzaram, o que indica que o elemento procurado não está no arranjo de entrada. Entretanto, na versão iterativa do código essa verificação é feita no laço
whileque é usado para percorrer o arranjo. -
Ajuste do espaço de busca: dentro do laço
while, fazemos o palpite de onde o elemento procurado pode estar. Como anteriormente, supomos que ele estará no meio do arranjo. A seguir, caso o palpite não esteja correto, ajustamos os limites esquerdo e direito da parte do arranjo que estamos analisando. Na versão recursiva do algoritmo, a cada chamada recursiva reduzíamos o espaço de busca pela metade. Na versão iterativa fazemos essa redução no espaço de busca a cada iteração do laçowhile. Assim, na versão recursiva tinhamos no máximo $O(\log n)$ chamadas de função, ao passo que na versão iterativa temos no máximo $O(\log n)$ iterações do laço.
Uma coisa que não mencionamos mas convém ressaltar é que Python possui um módulo que nos permite implementar pesquisa facilmente. Esse módulo se chama bisect, que é usado para manter uma lista ordenada sem ter que reordenar a lista após cada inserção. Vejamos um exemplo de implementação de pesquisa binária usando bisect:
import bisect
def pesquisa_binaria_bisect(A, item):
"""Implementa pesquisa binária usando bisect."""
# Encontra o ponto onde o item deveria ser (ou está) inserido.
i = bisect.bisect_left(A, item)
# Testa se o item está na lista.
return i if i < len(A) and A[i] == item else -1
A = [0, 10, 20, 30, 40, 50, 60, 70]
print("Pesquisa com sucesso:", pesquisa_binaria_bisect(A, 20))
print("Pesquisa com sucesso:", pesquisa_binaria_bisect(A, 0))
print("Pesquisa com sucesso:", pesquisa_binaria_bisect(A, 70))
print("Pesquisa com falha:", pesquisa_binaria_bisect(A, 100))Pesquisa com sucesso: 2 Pesquisa com sucesso: 0 Pesquisa com sucesso: 7 Pesquisa com falha: -1
O módulo bisect pode ser útil no dia a dia para facilitar tarefas que envolvam pesquisa binária, mas como nosso foco aqui é em aprender algoritmos, tentaremos sempre implementar nossa própria versão dos algoritmos explicados.
Vejamos agora alguns exercícios que usam pesquisa binária.
Exercícios
-
Proponha uma estratégia para o Jogo das Perguntas. Nesse jogo, um jogador pensa em um número no intervalo de 1 a n. O outro jogador tenta adivinhar o número fazendo perguntas do tipo: "o número é menor/maior que X?" O objetivo do jogo é descobrir o número fazendo o menor número possível de perguntas. Assuma que ninguém trapaceia, isto é, a pessoa que responde cada pergunta fala a verdade.
Clique para ver a solução
Este exercício ilustra uma aplicação direta de busca binária. Para resolvê-lo, basta fazer uma busca binária pelo número desejado e ir ajustando os intervalos a cada pergunta. Suponha que n seja 100. A primeira pergunta que devemos fazer é o número procurado é menor que 50? Se sim, ajustamos o intervalo de busca para os números de 1 a 49 e repetimos o procedimento. Essa estratégia nos permite encontrar o número desejado em $O(log n)$ perguntas.
-
Qual seria sua estratégia se n fosse desconhecido, ou seja, se o número escolhido puder ser qualquer inteiro positivo.
Clique para ver a solução
Para resolver esse problema, podemos usar a estratégia usada no exercício anterior, ou seja, podemos fazer uma pesquisa binária simples pelo número desejado. Entretanto, não sabemos o intervalo superior da busca binária. Para descobri-lo, podemos usar o seguinte raciocínio. Começamos perguntando: "n é maior que 1?" Se sim, perguntamos: "n é maior que 2?" Se sim, perguntamos: "n é maior que 4?" E assim por diante, sempre dobrando o tamanho. Com isso, descobriremos o valor de n em $O(log n)$ perguntas. A seguir, de posse do valor de n, basta empregarmos a mesma estratégia usada no exercício anterior.
-
Pesquise por um elemento igual ao índice. O problema a ser resolvido pode ser definido da seguinte maneira:
-
Descrição da entrada: Uma sequência ordenada $S$ de $n$ números inteiros distintos e um elemento desejado $e$.
-
Descrição da tarefa: Determinar se existe um elemento $i$ tal que $S[i] = i$.
-
Descrição da saída: Se o elemento estiver na sequência, retorne o índice em que o elemento aparece em $S$. Caso contrário, retorne o valor $-1$.
-
Clique para ver a solução
Nosso objetivo neste exercício é tentar encontrar uma adaptação do algoritmo de busca binária que nos permita encontrar um elemento em uma sequência que possui valor igual ao índice em que ele se encontra. Na verdade, é possível fazermos uma modificação simples no algoritmo de busca binária para resolver o problema em questão.
Para efeitos de simplificação, suponha que o arranjo de entrada possua tamanho par. Calcule a diferença $d = n/2 - S[n/2]$. Se tivermos $d = 0$, encontramos um elemento cujo valor é igual ao índice em que ele se encontra, e a tarefa está terminada.
Caso contrário, temos duas opções a considerar: a primeira opção é se $d > 0$, e a segunda opção é se $d < 0$. Se $d > 0$, como todos os números são distintos, o valor de $S[n/2] - 1$ é menor que $n/2 - 1$, e assim por diante. Assim, nenhum número na primeira metade do arranjo pode satisfazer a propriedade desejada, então devemos concentrar nossa busca na segunda metade do arranjo. Argumento análogo vale para o caso em que $d > 0$. Vejamos uma implementação desta ideia, juntamente com testes para verificar o correto funcionamento dela.
import random
def procura_entrada_igual_ao_indice(A):
"""Usa busca binária para encontrar um elemento igual ao índice."""
esquerda, direita = 0, len(A) - 1
while esquerda <= direita:
meio = (esquerda + direita) // 2
diferenca = A[meio] - meio
if diferenca == 0:
return meio
elif diferenca > 0:
direita = meio - 1
else: # diferenca < 0.
esquerda = meio + 1
return -1
def procura_entrada_igual_ao_indice_linear(A):
"""Usa busca sequencial para encontrar um elemento igual ao índice."""
for i, a in enumerate(A):
if a == i:
return i
return -1
def testa_procura_entrada_igual_ao_indice():
for _ in range(1000):
# Gera o tamanho da lista aleatoriamente.
n = random.randint(1, 1000)
# Gera a sequência de números aleatoriamente.
A = random.sample(range(0, 1000), n)
# Ordena a sequência.
A.sort()
# Obtém resposta usando pesquisa binária.
res_busca_binaria = procura_entrada_igual_ao_indice(A)
# Verifica resposta.
if res_busca_binaria != -1:
assert res_busca_binaria == A[res_busca_binaria]
else:
assert res_busca_binaria == procura_entrada_igual_ao_indice_linear(A)
print("Sucesso!")
testa_procura_entrada_igual_ao_indice()Sucesso!
-
Busca binária em uma lista ordenada rotacionada. O problema, retirado do livro "Introduction to Algorithms: A Creative Approach", escrito por Udi Manber, pode ser definido da seguinte maneira:
-
Descrição da entrada: Uma sequência ordenada rotacionada $S$ de $n$ números inteiros. Um exemplo de lista ordenada rotacionada é $[5, 6, 7, 1, 2, 3, 4]$.
-
Descrição da tarefa: Encontre o menor elemento da sequência $S$. Para simplificar a implementação, assuma que só existe um menor elemento na sequência $S$.
-
Descrição da saída: Retorne o índice $i$ em que o elemento aparece em $S$.
-
Clique para ver a solução
Para encontrar o menor elemento $x_{i}$ da sequência, podemos usar uma modificação do algoritmo de pesquisa binária. Primeiro, usamos pesquisa binária para eliminar metade da sequência. Escolha dois números quaisquer $x_{k}$ e $x_{m}$ tais que $k < m$. Se $k < m$, então $i$ não pode estar no intervalo $k \leq i \leq m$, uma vez que $x_{i}$ é o menor elemento da sequência. Por outro lado, se $x_{k} > x_{m}$, então $i$ tem que estar no intervalo $k \leq i \leq m$, uma vez que a ordem dos elementos foi trocada em algum lugar nesse intervalo. Vejamos uma implementação desta ideia.
import random
def encontra_minimo(A, esquerda, direita):
"""Usa busca binária para encontrar o menor
elemento em uma lista ordenada rotacionada."""
# A sequência de entrada pode não estar rotacionada.
if direita < esquerda:
return A[0]
# Só há um elemento restante.
if direita == esquerda:
return A[esquerda]
meio = (esquerda + direita) // 2
# Verifica se elemento A[meio + 1] é o menor.
if meio < direita and A[meio + 1] < A[meio]:
return A[meio + 1]
# Verifica se elemento A[meio] é o menor.
if meio > esquerda and A[meio] < A[meio - 1]:
return A[meio]
# Decide qual metade do arranjo verificar.
if A[direita] > A[meio]:
return encontra_minimo(A, esquerda, meio - 1)
else:
return encontra_minimo(A, meio + 1, direita)
def testa_encontra_minimo():
for _ in range(1000):
# Gera a sequência de números aleatoriamente.
A = list(set(random.sample(range(-1000, 1000), 1000)))
# Ordena lista.
A.sort()
# Tamanho da lista.
n = len(A)
# Encontra ponto para rotacionar a lista.
k = random.randint(1, n)
# Rotaciona a lista.
A = A[k:n] + A[0:k]
# Verifica resposta.
assert encontra_minimo(A, 0, len(A) - 1) == min(A)
print("Sucesso!")
testa_encontra_minimo()Sucesso!
Como vimos nesta seção, a pesquisa binária nos permite procurar por elementos em uma sequência com complexidade logarítmica. Entretanto, ela exige que a sequência de entrada esteja ordenada. Uma pergunta que podemos fazer é: dada uma sequência de números, como podemos ordená-la de forma eficiente? Na próxima seção descrevemos algoritmos para ordenar sequências de elementos de forma eficiente.
Discussão
Nesta seção, listaremos algumas questões a serem consideradas quando você tiver que implementar uma rotina de pesquisa. Apesar dos benefícios da pesquisa binária em termos de eficiência, há casos em que ela pode não ser a melhor opção.
-
Quanto tempo você tem para implementar sua rotina de pesquisa? Pesquisa binária é um algoritmo difícil de ser implementado, pois possui muitos detalhes e casos especiais nos quais é fácil cometer erros. Se você tem 10 minutos para implementar sua rotina de pesquisa, pode ser melhor implementar pesquisa sequencial do que se aventurar em uma implementação de pesquisa binária que possivelmente conterá bugs.
-
O vetor de entrada é pequeno? Se o vetor de entrada for pequeno a pesquisa linear provavelmente será mais eficiente. Para entradas grandes, os benefícios da pesquisa binária se tornam mais evidentes (veja figura acima sobre pesquisa linear versus pesquisa binária).
-
O vetor de entrada já está ordenado? Se o vetor de entrada tiver sido previamente ordenado, isto é, se você não tiver que pagar o preço de ordenar o vetor para depois realizar buscas, então o melhor a se fazer é usar pesquisa binária.
Playground
# Use este espaço para praticar o que você aprendeu nesta seção.
# Basta digitar o código no espaço abaixo e clicar 'run'.