Na seção anterior, explicamos brevemente como determinar aproximadamente o número de operações que um algoritmo executa. O processo foi um pouco trabalhoso porque queríamos ilustrar como as coisas funcionam quando não possuímos ferramental teórico nenhum. Entretanto, com um pouco de prática e com as ferramentas certas, fica muito mais fácil analisar a complexidade assintótica de algoritmos. Nesta seção, explicaremos a principal ferramenta usada em análise de complexidade e incluiremos alguns exercícios para que você pratique os conceitos aprendidos.

A principal ferramenta usada para se analisar a complexidade assintótica de algoritmos é chamada notação big-oh (ou simplesmente notação $O$). A notação $O$, quando aplicada a um algoritmo, nos fornece um limite superior para o tempo de execução desse algoritmo. A notação big-oh é uma notação universal para se falar de desempenho de algoritmos.

No nosso exemplo da seção anterior, poderíamos dizer que o algoritmo_a possui complexidade $O(n^2)$, e o algoritmo_b possui complexidade $O(n)$. Mas o que isso quer dizer exatamente?

Ao dizer que um algoritmo é $O(n)$, estamos dizendo que existe uma constante positiva $c$ pela qual podemos multiplicar $n$, e esta nova função $g(n) = c \times n$ é um limite superior para o tempo de execução do algoritmo em questão. Graficamente, temos a seguinte situação:

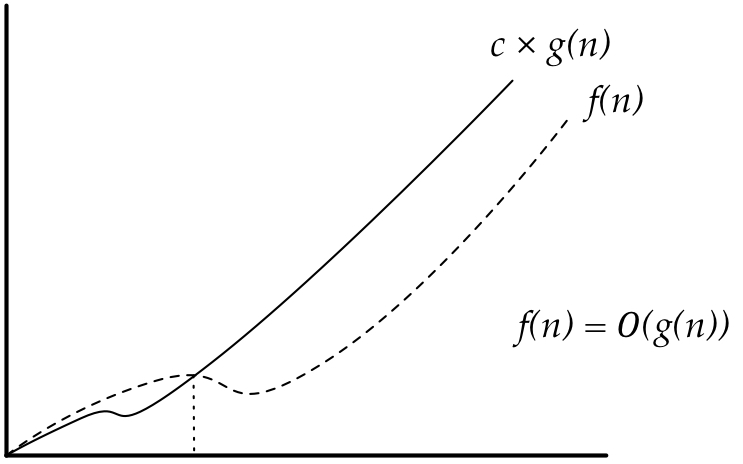
Pelo gráfico, podemos chegar a uma definição mais formal da função $O$:

Definição: Dizer que $f(n) = O(g(n))$ significa que existe constante positiva $c$ tal que $f(n) \leq c \times g(n)$, para algum $n$ maior que $n_{0}$. O ponto $n_{0}$ é o ponto no gráfico acima em que a curva da função $f(n)$ intercepta a curva da função $g(n)$.

No nosso exemplo anterior, podemos dizer que o algoritmo_a é $O(n)$ porque, dado que sabemos que ele executa cerca de $n$ operações, podemos escolher uma constante positiva $c = 2$, de modo que $g(n) = c \times n$ sempre será maior que $f(n) = n$. O mesmo raciocínio pode ser aplicado ao algoritmo_b para concluir que ele possui complexidade $O(n^2)$.

Ao analisar o gráfico acima, vemos que a função $g(n)$ cresce mais rapidamente que $f(n)$, pois a curva de $g(n)$ está acima da de $f(n)$, a partir de um dado valor de $n$. Quando isso acontece, costumamos dizer que $g(n)$ domina assintoticamente $f(n)$, ou que $g(n)$ é assintoticamente superior a $f(n)$. Matematicamente esta afirmação nos diz que $\lim_{n\to\infty} \frac{g(n)}{f(n)} = \infty$.

Uma outra forma de entender a notação $O$ é em termos de comparações. Se uma função $f(n)$ é $O(g(n))$, podemos dizer que $f(n) \leq g(n)$.

Além de comparações com menor que e maior que, a notação $O$ nos permite realizar operações matemáticas entre duas funções de complexidade. As operações mais comuns a serem realizadas são a soma e a multiplicação:

As regras acima não podem ser estendidas para subtração e divisão.

A função $O$ é usada quando desejamos encontrar o limite superior do tempo de execução de um algoritmo. Entretanto, em algumas situações, isso não é o suficiente. Existem situações em que precisamos dizer qual o limite inferior do tempo de execução de um algoritmo. Para isso, usamos a função Ômega, representada por $\Omega$, que pode ser definida assim:

Definição: Dizer que $f(n) = \Omega(g(n))$ significa que existe constante positiva $c$ tal que $g(n) \leq c \times f(n)$.

Além disso, se uma função $f(n)$ satisfaz tanto $f(n) = O(g(n))$ e $f(n) = \Omega(g(n))$, então dizemos que $f(n) = \Theta(g(n))$ (leia-se: "theta"). A função $\Theta$ nos fornece um limite inferior e superior, ou seja, um limite mais firme e preciso, para o tempo de execução de um algoritmo.

As funções $O$, $\Theta$, e $\Omega$ correspondem, grosso modo, a $\leq$, $=$, e $\geq$. Existem também funções que correspondem a $<$ e $>$, são elas: $o$ e $\omega$, respectivamente. Essas funções, entretanto, não são muito usadas na prática e por isso quase não falaremos sobre elas durante este curso.