Representação de Grafos
Na seção anterior, vimos os conceitos principais sobre grafos e aprendemos como eles podem ser visualizados. Nesta seção veremos como eles podem ser representados em um programa de computador.
A melhor representação para um grafo depende do que desejamos fazer com ele e do quão denso ou esparso ele é. Grafos esparsos são grafos que possuem um pequeno número de arestas em relação ao número de vértices, ao passo que em grafos densos o número de arestas se aproxima do máximo de arestas possível.
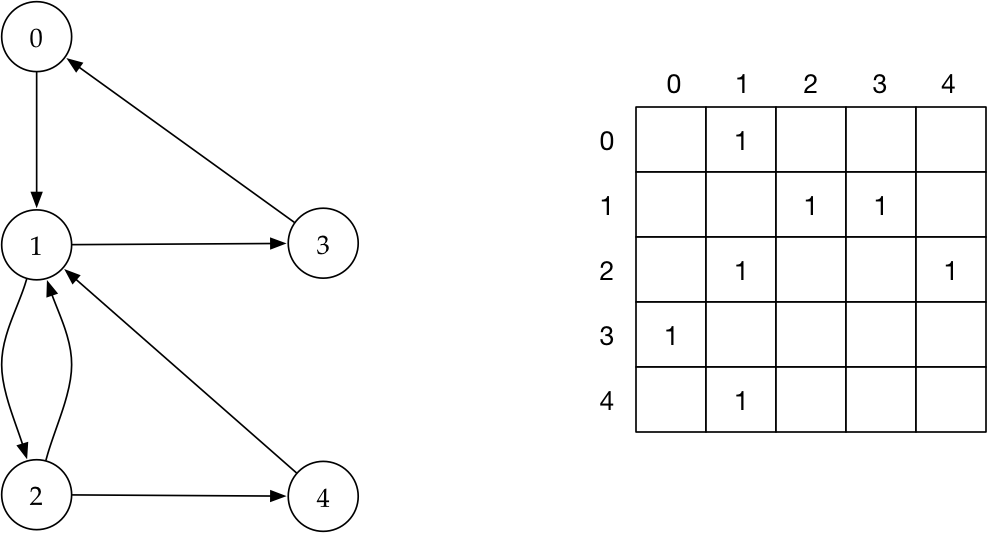
Existem duas representações principais para grafos. A primeira é chamada matriz de adjacências, que nada mais é do que uma matriz $M$ de $n$ linhas e $n$ colunas em que $M[i, j] = 1$ se existe uma aresta do vértice $i$ para o vértice $j$. Lembre-se que estamos seguindo a convenção de que $n$ representa o número de vértices do grafo.
Se estivermos representando um grafo não-direcionado e existir uma aresta entre os vértices $i$ e $j$, então teremos tanto $M[i, j] = 1$ quanto $M[j, i] = 1$. Em outras palavras, a matriz de adjacências $M$ que representa um grafo não-direcionado é simétrica. Nessa representação, o tempo gasto para determinar se um vértice $u$ é vizinho de um vértice $v$ é constante, pois basta verificarmos se $M[u, v]$ é igual a $1$.
Vejamos um exemplo de grafo e sua matriz de adjacências.
A segunda representação é chamada lista de adjacências, e consiste de um arranjo (ou lista) $A$ com $n$ nodos em que $A[i]$ contém a lista de vizinhos do vértice $i$. Se o grafo for direcionado, os vizinhos de um vértice $v$ serão somente aqueles vértices para os quais existe uma aresta saindo de $v$. Nessa representação, o tempo gasto para determinar se um vértice $u$ é vizinho de um vértice $v$ é proporcional ao grau de saída do vértice $v$, ou seja, ao número de arestas que saem de $v$.
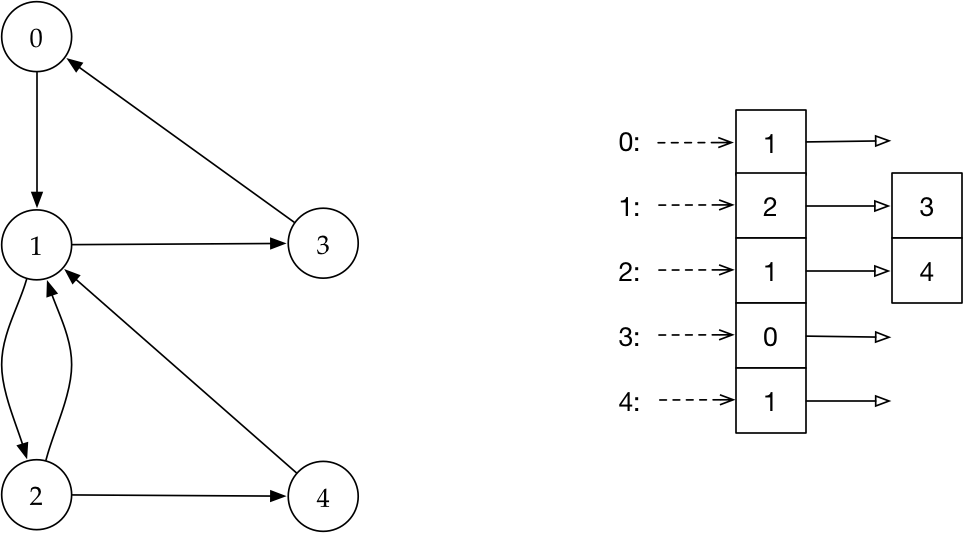
Se o grafo a ser representado for relativamente esparso, a lista de adjacências oferecerá uma representação mais compacta (econômica) do grafo porque ela conterá somente as conexões existentes entre vértices.
Representando Grafos em Python
Como listas de adjacência são a forma mais comum de se representar grafos, nosso foco nesta seção será em como implementar um grafo em Python usando essa estrutura de dados.
Nesta seção veremos duas formas simples de representar listas de adjacência em Python. Uma delas, que chamamos de representação explícita, armazena os nomes dos vértices no próprio grafo. A outra, chamada representação implícita, assume que cada vértice possui um identificador inteiro, e faz referência aos vértices por meio desse identificador.
Antes de discutirmos as formas de representar grafos, convém esclarecermos como montamos o grafo em si. Em nossos exemplos, assumiremos que nos será fornecida uma lista com as ligações entre vértices (uma lista de arestas), a partir da qual criaremos os vértices e as arestas que os conectam. Nos exemplos abaixo, trabalharemos com a seguinte lista de arestas:
A B B C B D C B C E D A E B
Na lista acima, existe uma aresta saindo do vértice à esquerda e chegando no vértice à direita. Por exemplo, a aresta A B significa que existe uma aresta saindo do vértice A e chegando no vértice B.
Vejamos como representar o grafo descrito pela lista de arestas acima.
Representação Explícita
De uma forma bem simples, podemos representar um grafo em Python assim:
grafo = { "A" : ["B"],
"B" : ["C", "D"],
"C" : ["B", "E"],
"D" : ["A"],
"E" : ["B"]
}O código acima representa o grafo como um dicionário de listas. Ele nos diz que existe uma aresta do vértice A para o vértice B, uma aresta do vértice B para os vértices C e D, e assim por diante. A figura abaixo mostra o grafo representado pelo código acima.
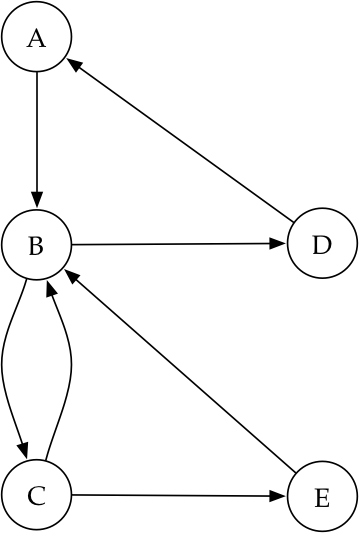
O interessante de se usar um dicionário para representar o grafo é a conveniência que isso proporciona. As chaves do dicionário são os vértices e os valores são as listas de adjacências. Para iterar sobre cada vértice v de um grafo G, precisamos simplesmente fazer for v in G. E para iterar sobre os vizinhos de um vértice v, basta fazer for u in G[v].
Outra alternativa é representar o grafo como um dicionário de conjuntos. Na prática, muito pouca coisa muda em relação à representação acima, mas se usarmos um conjunto em vez de uma lista garantimos que não existirão arestas duplicadas entre dois nodos – algo que assumimos para todos os grafos com que trabalharemos nos exemplos.
Antes de avançarmos, é muito importante mencionar que se você precisa criar e manipular um grafo em Python de forma simples e rápida, a forma mostrada acima é provavelmente sua melhor opção. A maioria dos algoritmos em grafos pode ser implementada usando essa estrutura como base. Ela também é provavelmente a melhor opção caso você não precise fazer nada muito sofisticado (como ter programas externos acessando sua implementação de grafo, por exemplo). Nas seções seguintes, trabalharemos com essa implementação simples de grafo.
Porém, se você deseja algo mais elaborado, você pode criar uma classe para representar seu grafo, como explicamos a seguir.
Criando uma Classe para Representar Grafos em Python
Dado um grafo qualquer, precisamos realizar operações sobre ele. As operações mais comuns são obter a lista de vértices do grafo, obter a lista de arestas, verificar se existe uma aresta entre dois vértices, adicionar uma aresta entre dois vértices, etc. No exemplo abaixo, criamos uma classe Grafo na qual implementamos essas e outras operações.
from collections import defaultdict
class Grafo(object):
""" Implementação básica de um grafo. """
def __init__(self, arestas, direcionado=False):
"""Inicializa as estruturas base do grafo."""
self.adj = defaultdict(set)
self.direcionado = direcionado
self.adiciona_arestas(arestas)
def get_vertices(self):
""" Retorna a lista de vértices do grafo. """
return list(self.adj.keys())
def get_arestas(self):
""" Retorna a lista de arestas do grafo. """
return [(k, v) for k in self.adj.keys() for v in self.adj[k]]
def adiciona_arestas(self, arestas):
""" Adiciona arestas ao grafo. """
for u, v in arestas:
self.adiciona_arco(u, v)
def adiciona_arco(self, u, v):
""" Adiciona uma ligação (arco) entre os nodos 'u' e 'v'. """
self.adj[u].add(v)
# Se o grafo é não-direcionado, precisamos adicionar arcos nos dois sentidos.
if not self.direcionado:
self.adj[v].add(u)
def existe_aresta(self, u, v):
""" Existe uma aresta entre os vértices 'u' e 'v'? """
return u in self.adj and v in self.adj[u]
def __len__(self):
return len(self.adj)
def __str__(self):
return '{}({})'.format(self.__class__.__name__, dict(self.adj))
def __getitem__(self, v):
return self.adj[v]Alguns comentários sobre a implementação acima:
-
Ela nos permite criar tanto grafos direcionados quanto não direcionados, por meio do parâmetro
direcionadousado ao criar o grafo. -
Ela assume que todas as arestas possuem peso 1, ou seja, o grafo é não-ponderado. Em breve mostraremos como implementar grafos ponderados.
-
Implementamos dois métodos mágicos:
lenestr. Estes métodos são implementados para fazer com que o acesso à nossa estrutura de dados seja feito como o acesso a estruturas de dados padrão do Python. Por exemplo, para que sejamos capazes de obter o tamanho do grafo usandolen(grafo), precisamos implementar o métodolen. Caso contrário, precisaríamos fazerlen(grafo.adj), mas isso é ruim porque ao fazer isso estamos acessando a implementação do grafo em si. Se essa implementação mudar no futuro (se o nomeadjmudar, por exemplo) nosso código não funcionará mais. Para prevenis quanto a acessos à implementação do grafo, precisamos prover métodos acessórios, como fizemos. Para que possamos fazerprint(grafo)e obter algo legível, precisamos implementar o métodostr. E para que ao fazergrafo[v]obtenhamos a lista de adjacências do vérticev, precisamos implementar o métodogetitem. Veja mais detalhes sobre esse tipo de método aqui.
Vejamos como criar e imprimir um grafo.
# Cria a lista de arestas.
arestas = [('A', 'B'), ('B', 'C'), ('B', 'D'), ('C', 'B'), ('C', 'E'), ('D', 'A'), ('E', 'B')]
# Cria e imprime o grafo.
grafo = Grafo(arestas, direcionado=True)
print(grafo.adj)defaultdict(<class 'set'>, {'A': {'B'}, 'B': {'C', 'D'}, 'C': {'B', 'E'}, 'D': {'A'}, 'E': {'B'}})
Vejamos agora como usar algumas das funções da classe Grafo implementada acima.
print(grafo.get_vertices())['A', 'B', 'C', 'D', 'E']
print(grafo.get_arestas())[('A', 'B'), ('B', 'C'), ('B', 'D'), ('C', 'B'), ('C', 'E'), ('D', 'A'), ('E', 'B')]
print(grafo.existe_aresta('A', 'B'), grafo.existe_aresta('E', 'C'))True False
Representação Implícita
A diferença entre a representação explícita e a implícita é que nesta cada vértice recebe automaticamente um identificador inteiro enquanto naquela o nome de um vértice é definido arbitrariamente. Vejamos um exemplo de grafo representado implicitamente.
grafo = [ [1], # Vizinhos do vértice 0.
[2, 3], # Vizinhos do vértice 1.
[1, 4], # Vizinhos do vértice 2.
[0], # Vizinhos do vértice 3.
[1] # Vizinhos do vértice 4.
]O grafo acima mostra uma representação equivalente à do grafo com o qual vínhamos trabalhando até agora (o vértice 0 é equivalente ao A, o vértice 1 ao B, e assim por diante). Veja abaixo uma figura ilustrando esse grafo.
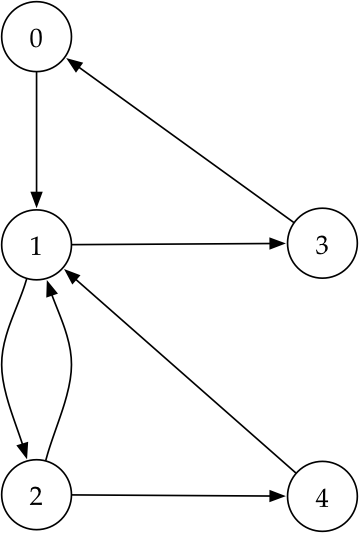
Como exercício, veja se consegue adaptar a implementação da classe Grafo para essa nova representação. Aqui está uma sugestão de implementação. Basicamente, a única coisa que muda é a declaração da lista de adjacências. Antes, ela era declarada assim:
self.adj = defaultdict(set)Agora, essa mesma estrutura pode ser declarada assim:
self.adj = [[] for _ in range(num_vertices)]Note que, como estamos representando cada vértice do grafo por um identificador inteiro (a posição do vértice na estrutura adj), precisamos saber de antemão o número de vértices do grafo para inicializar a lista de adjacências. Na prática, a implementação usando dicionário é mais prática, mas pode ser mais lenta em alguns casos, pois, apesar complexidade de se acessar um elemento em um dicionário ser constante (como ocorre com as listas em Python), no pior caso essa complexidade é linear no tamanho do dicionário.
Veja abaixo como criar e imprimir um grafo com essa nova implementação de listas de adjacência. A utilização do restante das funções que implementamos anteriormente não muda.
Agora que já sabemos como representar grafos em Python, precisamos entender como criar algoritmos que operem sobre esses grafos.
Playground
# Use este espaço para praticar o que você aprendeu nesta seção.
# Basta digitar o código no espaço abaixo e clicar 'run'.