Algoritmos em Grafos
Grafos são importantíssimos em Ciência da Computação. Eles aparecem, por exemplo, na modelagem de problemas envolvendo distâncias entre pontos em um mapa, na modelagem de redes sociais, de ligações (links) entre páginas na Internet, e em inúmeros outros cenários.

Dada a importância de grafos em Ciência da Computação, saber modelar problemas usando grafos e dominar os algoritmos que operam sobre grafos são habilidades extremamente úteis para um programador. Feita esta propaganda inicial, podemos partir de fato para nosso estudo de algoritmos em grafos.
O nome grafo pode parecer estranho, mas grafos são, na verdade, coisas relativamente simples. A primeira coisa a se saber é que um grafo é diferente de um gráfico, aquela coisa com o eixo $x$ e o eixo $y$ que a gente estuda em matemática. Um grafo, por sua vez, nada mais é do que um conjunto de vértices (que em nos nossos desenhos de grafos serão representados como bolinhas) conectados por arestas (que em nos nossos desenhos serão representadas por linhas ou setas). Assim, um grafo representa relacionamentos (expressados pelas arestas) entre um conjunto de entidades (os vértices).
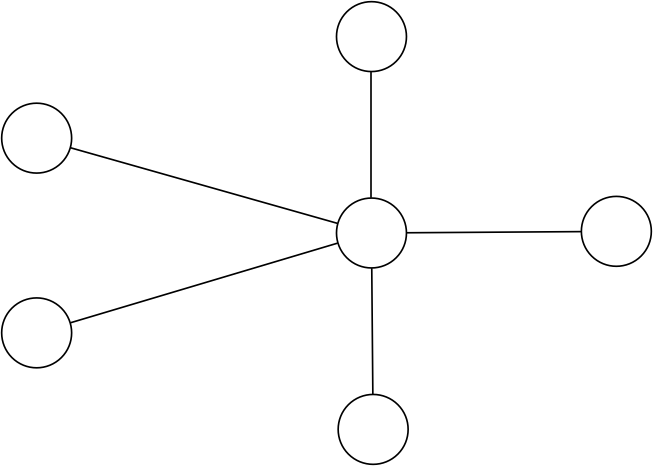
O interessante de grafos é que com algo aparentemente simples conseguimos modelar uma multitude de problemas interessantes. Por exemplo, suponha que desejemos representar as ruas e esquinas de uma cidade como um grafo. Para isso, basta considerarmos as esquinas como vértices e as ruas como arestas. Com essa modelagem simples, podemos, por exemplo, determinar, dadas as esquinas A e B, qual é o número mínimo de esquinas pelas quais precisamos passar para ir de A até B. Um exemplo de grafo como o que acabamos de descrever é mostrado abaixo.
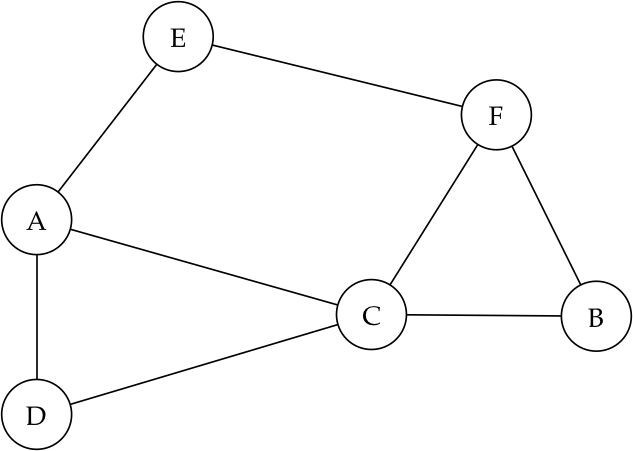
Definições
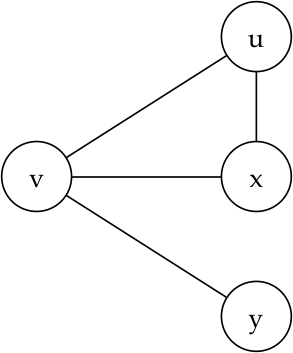
Como dissemos anteriormente, um grafo consiste de um conjunto de vértices (ou nodos) com arestas conectando alguns deles. Usaremos $V$ para nos referir ao conjunto de vértices de um grafo e $E$ para nos referir ao conjunto de arestas. Se existe uma aresta entre dois vértices, dizemos que esses vértices são vizinhos. O grau de um vértice é o número de vizinhos que ele possui. Na figura abaixo, os seguintes pares de vértices são vizinhos: (v, u), (v, x), (v, y), e (u, x).
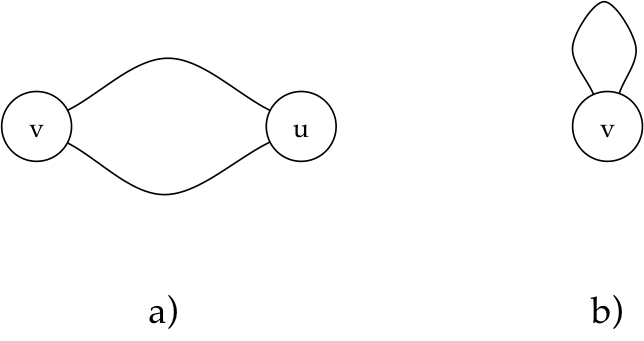
A menos que especifiquemos o contrário, os grafos com os quais lidaremos não possuem múltiplas arestas entre os mesmos vértices (multi-arestas) nem arestas saindo de um vértice e chegando nele mesmo (self-loops). A figura abaixo ilustra esses cenários.
Em geral, representamos o número de vértices de um grafo usando a letra $n$ e o número de arestas usando a letra $m$. De modo mais formal, temos $n = \left\vert{V}\right\vert$ (leia-se $n$ é igual à cardinalidade, ou tamanho, do conjunto de vértices) e $m = \left\vert{E}\right\vert$.
No grafo descrito acima (com vértices representando esquinas e arestas representando ruas), as conexões entre vértices são bidirecionais, ou seja, é possível usar uma rua tanto para ir quanto para vir de uma determinada esquina (as ruas são de mão dupla). Entretanto, é possível ter grafos em que as conexões entre vértices são unidirecionais. Tais grafos são chamados grafos direcionados, enquanto os outros (com conexões de mão dupla) são denominados grafos não-direcionados.
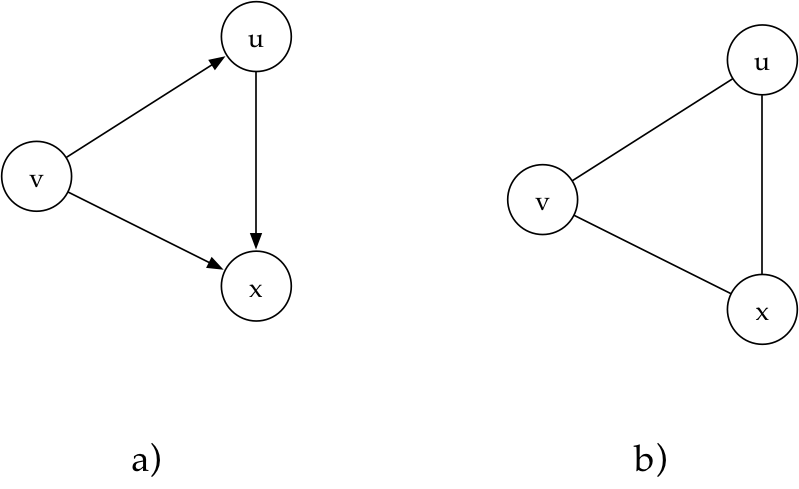
Até o momento, vimos como representar grafos de forma visual. Na próxima seção, aprenderemos representações computacionais destas estruturas.
Playground
# Use este espaço para praticar o que você aprendeu nesta seção.
# Basta digitar o código no espaço abaixo e clicar 'run'.