O algoritmo de busca em profundidade é percorrer todos os caminhos de um grafo de forma sistemática. Grosso modo, o algoritmo funciona assim. Começando por um vértice qualquer, e indo "o mais fundo possível". Sempre que encontramos um vértice já visitado, retornamos da busca.

A intuição aqui é parecida com a procura de um caminho entre a entrada e a saída de um labirinto. A cada ponto, escolhemos um caminho que pode nos levar até a saída. Se chegarmos a um beco sem saída ou a um caminho já visitado, precisamos retornar e tentar outro caminho.

Os algoritmos explicados nesta e nas próximas seções assumirão que o grafo de entrada é conectado e foi implementado usando listas de adjacência. Tomaremos como base a seguinte representação, discutida na seção anterior:

O código acima representa o grafo como um dicionário de listas. Ele nos diz que existe uma aresta do vértice 0 para o vértice 1, uma aresta do vértice B1 para os vértices 2 e 3, e assim por diante. Nesta implementação, para iterar sobre cada vértice v de um grafo, precisamos simplesmente fazer for v in grafo. E para iterar sobre os vizinhos de um vértice v, basta fazer for u in grafo[v].

A figura abaixo mostra o grafo representado pelo código acima.

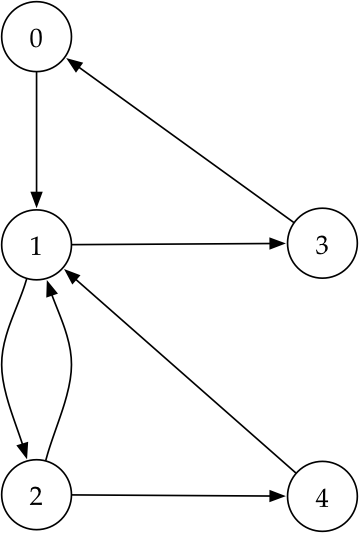
Tomando como base essa implementação de grafo e assumindo que exista uma estrutura de dados que nos permita manter registro dos vértices já visitados, discutiremos a seguir como implementar busca em profundidade neste grafo.

Porém, antes de partirmos para a implementação propriamente dita, tentaremos explicar de forma mais técnica o funcionamento da busca em profundidade. Ela começa a partir de um vértice arbitrário $r$, que é chamado de raiz da busca (esse vértice é também algumas vezes chamado de vértice fonte). O vértice $r$ é marcado como visitado. A seguir, seleciona-se um vértice qualquer $r_1$, dentre os vizinhos de $r$ que ainda não tenham sido marcados visitados, e uma nova DFS é iniciada recursivamente a partir dele. A recursão termina ao encontrar um vértice $v$ cujos vizinhos estejam todos marcados como visitados. Se após a DFS em $r_1$ terminar todos os outros vértices adjacentes a $r$ já tiverem sido marcados como visitados, a DFS em $r$ também termina. Caso contrário, seleciona-se um outro vértice arbitrário $r_2$ adjacente a $r$ e ainda não marcado como visitado. Uma nova DFS é iniciada em $r_2$. Esse procedimento é repetido até que todos os vértices do grafo tenham sido marcados como visitados.

Vejamos como implementar esse algoritmo que acabamos de descrever.

Note que, na implementação acima, passamos o conjunto visitados como parâmetro da função dfs_recursiva. É possível criar uma função adicional para encapsular esse parâmetro (e outros que viermos a precisar). Isso tornará nossa função mais elegante e genérica. Vejamos como criar essa função adicional.

Se quisermos melhorar ainda mais nossa implementação, podemos declarar a função dfs_recursiva dentro da função dfs. Ao fazer isso, não precisamos passar visitados como parâmetro para dfs_recursiva porque essa função já terá acesso ao conjunto de vértices visitados (como ambos estão dentro da função dfs, eles são visíveis dentro dessa função). A implementação pode ser feita como mostrado abaixo:

Assim, a busca em profundidade pode ser invocada da seguinte forma:

Se quisermos começar uma busca em profundidade de cada vértice do grafo que ainda não foi visitado, podemos modificar a função acima. Isso é útil, por exemplo, caso o grafo não seja conexo, ou seja, caso existam vértices no grafo que não podem ser alcançados a partir do vértice fonte, mas ainda assim desejamos visitá-los.

Veja como ficaria a função:

Assim, a busca em profundidade pode ser invocada da seguinte forma:

Nos exemplos abaixo, mostraremos como realizar busca em profundidade começando de um vértice específico, mas caso você deseje, pode modificá-los, seguindo o exemplo que acabamos de mostrar, para que a busca seja realizada em todo o grafo.

Podemos também implementar a função que realiza a busca em profundidade de forma iterativa, por questões de eficiência (funções iterativas tendem a ser mais eficientes). Veja abaixo uma sugestão de implementação:

A implementação acima usa uma pilha (falta_visitar) para manter registro da ordem em que devemos visitar os vértices. Uma forma de enxergar a função dessa pilha é como simulando a pilha de chamadas recursivas feitas ao invocarmos a função dfs_recursiva. Podemos também encapsular essa função dentro de outra para tornar a implementação mais elegante:

Em sua essência, a busca em profundidade funciona como mostrado na implementação acima. Porém, se observarmos bem o código acima, veremos que ele não faz nada muito interessante. Os vértices são visitados em uma ordem específica, e essa ordem é o que caracteriza a busca em profundidade. É importante frisar isso: a busca em profundidade determina uma ordem na qual os vértices do grafo são visitados.

Entretanto, dependendo do problema específico que desejamos resolver, podemos querer manter registro de certas coisas ao visitar os vértices. Por exemplo, na implementação acima nós não mantemos registro da ordem em que os vértices são visitados, mas isso poderia ser útil em alguns casos. Ou poderíamos retornar um valor específico caso chegássemos a um vértice pré-determinado (por exemplo, para dizer que um vértice é alcançável a partir de um vértice inicial). Nesses casos, temos duas opções: ou criamos estruturas de dados adicionais para armazenar essas informações (como fizemos ao criar uma estrutura para armazenar os vértices visitados), ou criamos uma classe para encapsular essas estruturas adicionais juntamente com o grafo.